三体問題をシミュレーションしてみた

はじめに

書籍の「三体」を読んでたら、三体問題をシミュレーションしたくなったのでやってみた！

「三体」読んでいるから、三体問題やってみた！おもしれえ#pyxel #python pic.twitter.com/EsgbhjimZv
— odanny🐶 (@dannyso16) April 15, 2025

三体問題は、三つの天体が互いに重力で引き合うときの運動を記述する問題。二体問題では楕円軌道が解析的に求められるけど、三体になると一般解が存在せず、カオス的な挙動を示す。らしい。

この動画では、三体問題のカオス的な挙動が非常にわかりやすく解説されてたので雰囲気をつかめると思う！

三体問題のカオス的な挙動を数値シミュレーションをしてみた。
微分方程式をやるのに、オイラー法とルンゲクッタ法が有名だと思うので、それを勉強してみた。

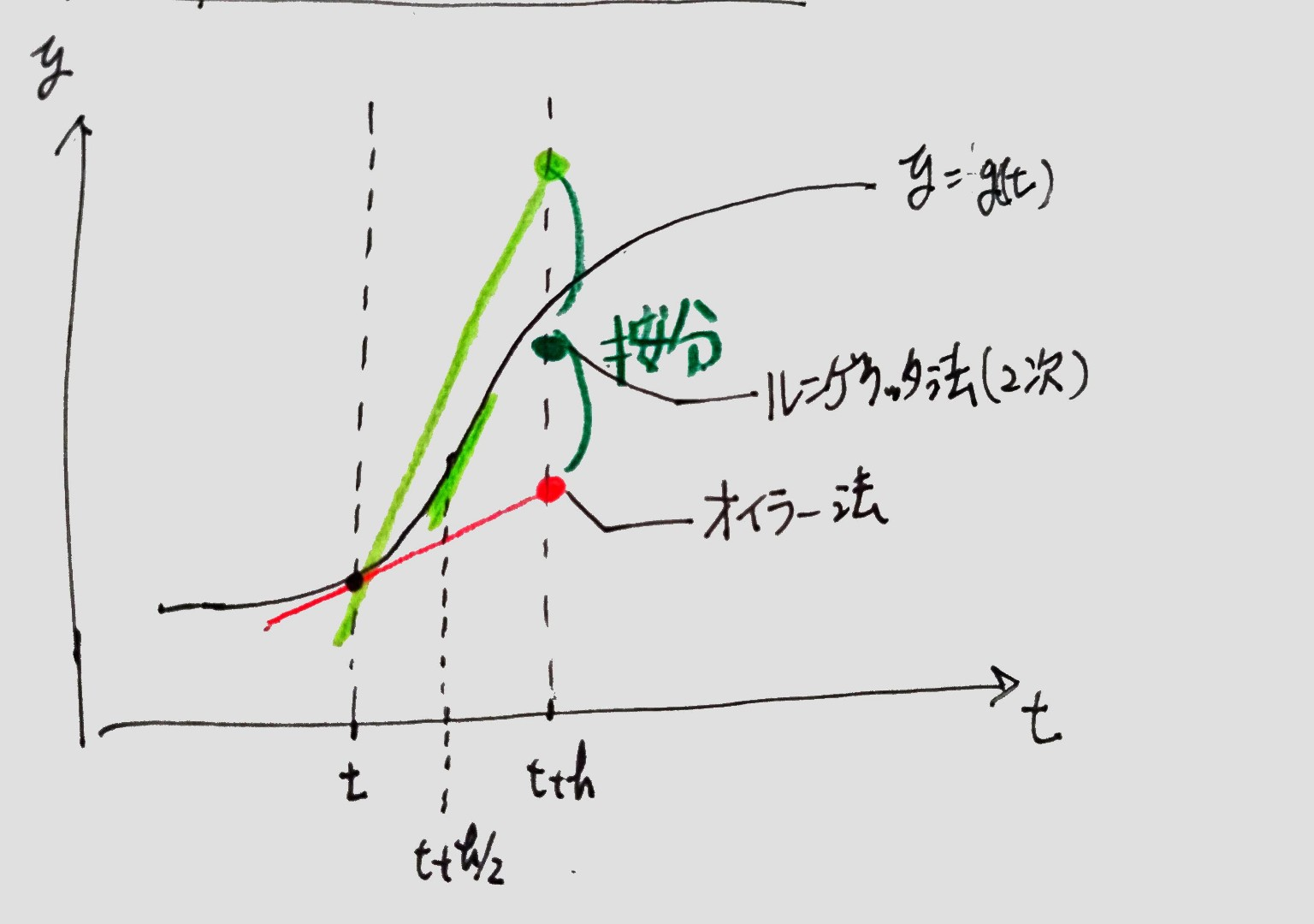
オイラー法と2次ルンゲクッタ法の比較

オイラー法はある時点の傾きを素直に信じて外挿するのに対して、ルンゲクッタ法はいくつかの地点で傾きを出したうえで重みづけして外挿する感じで精度が良い様子。「三体」に倣って、3つの恒星（黄、オレンジ、赤）と三体星でやってみる。（可視化はなんとなくpyxelを使った）

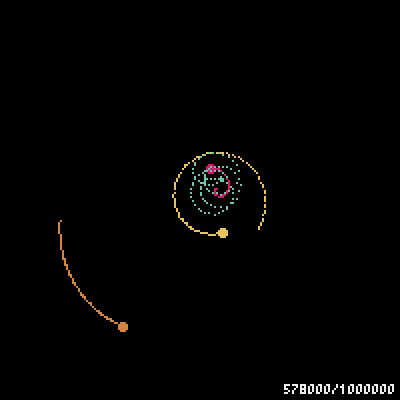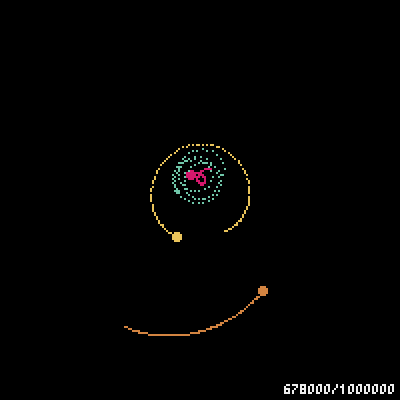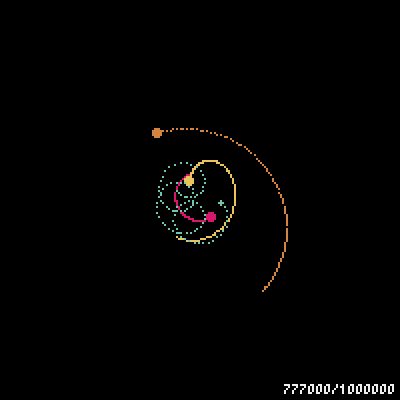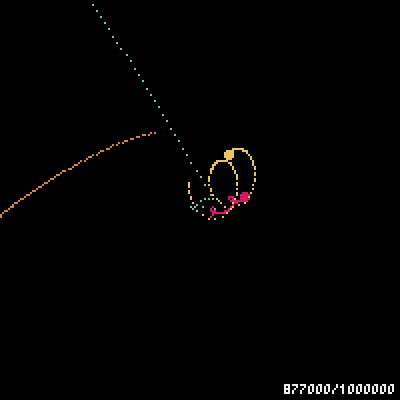
RKで斥力の問題が発生する例

gifの最後のほうで、三体の星が宇宙の彼方へ吹っ飛んで行ってしまった！さよなら三体星人。

どうやら恒星同士の距離が小さいときに斥力が大きくなりすぎる問題が発生して、吹っ飛んでしまうみたいだ。
具体的には、万有引力の法則に基づき、二つの天体間に働く力 $F$ は以下の式で表されている。

$$ F = G \frac{m_1 m_2}{r^2} $$

ここで、

距離 $r$ が小さくなると力 $F$ は急激に大きくなる。
このため、天体が非常に接近した場合、数値計算では誤差が増幅され、計算が不安定になるみたいだ。

この問題を解決するために、可変ステップルンゲ＝クッタ法（例：RKF45）を試してみた。
RKF45では、計算ステップ幅を動的に調整することで、効率的かつ安定した計算が可能になる。らしい。

仕組みはシンプルだ。1ステップで2つの異なる精度の解（たとえば4次と5次）を計算し、その差（推定誤差）を使ってステップ幅を調整する。

実装してみると、吹き飛ぶ問題は完全には解消されないものの、より長い間シミュレーションを安定して動かせるようになった。

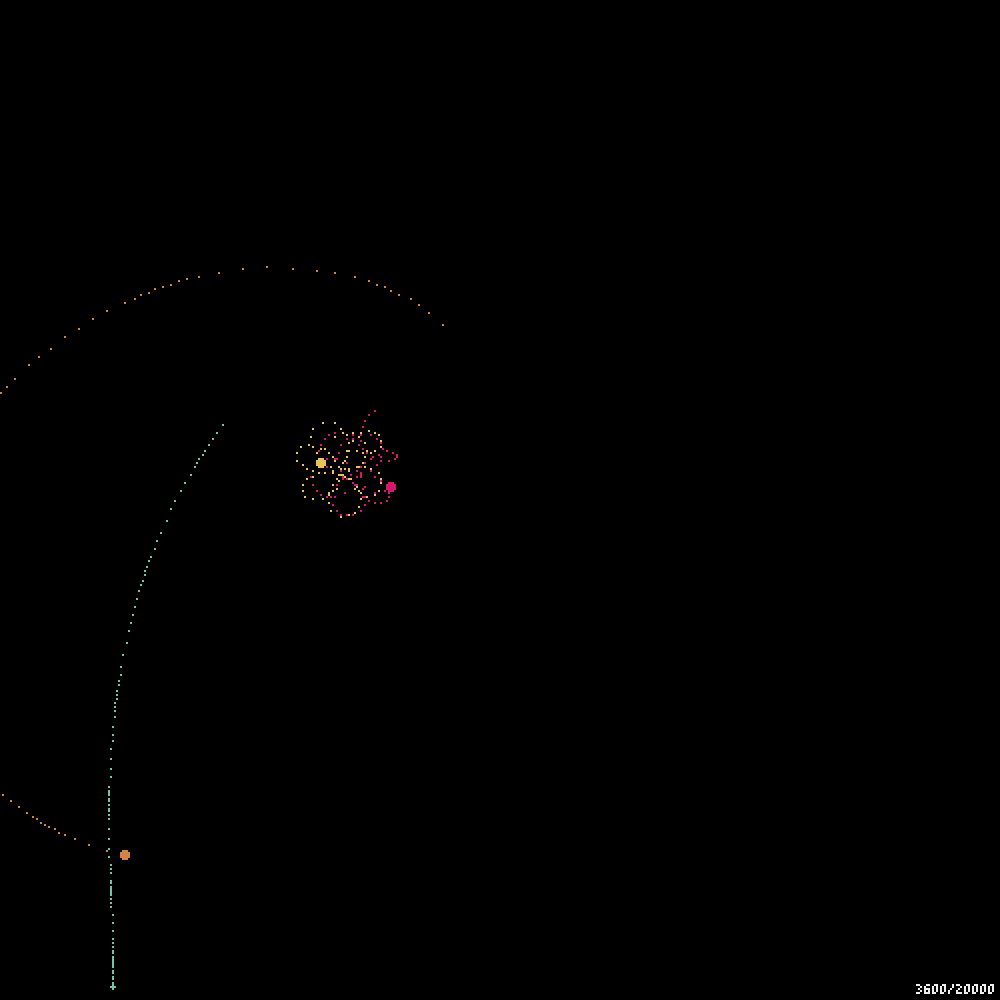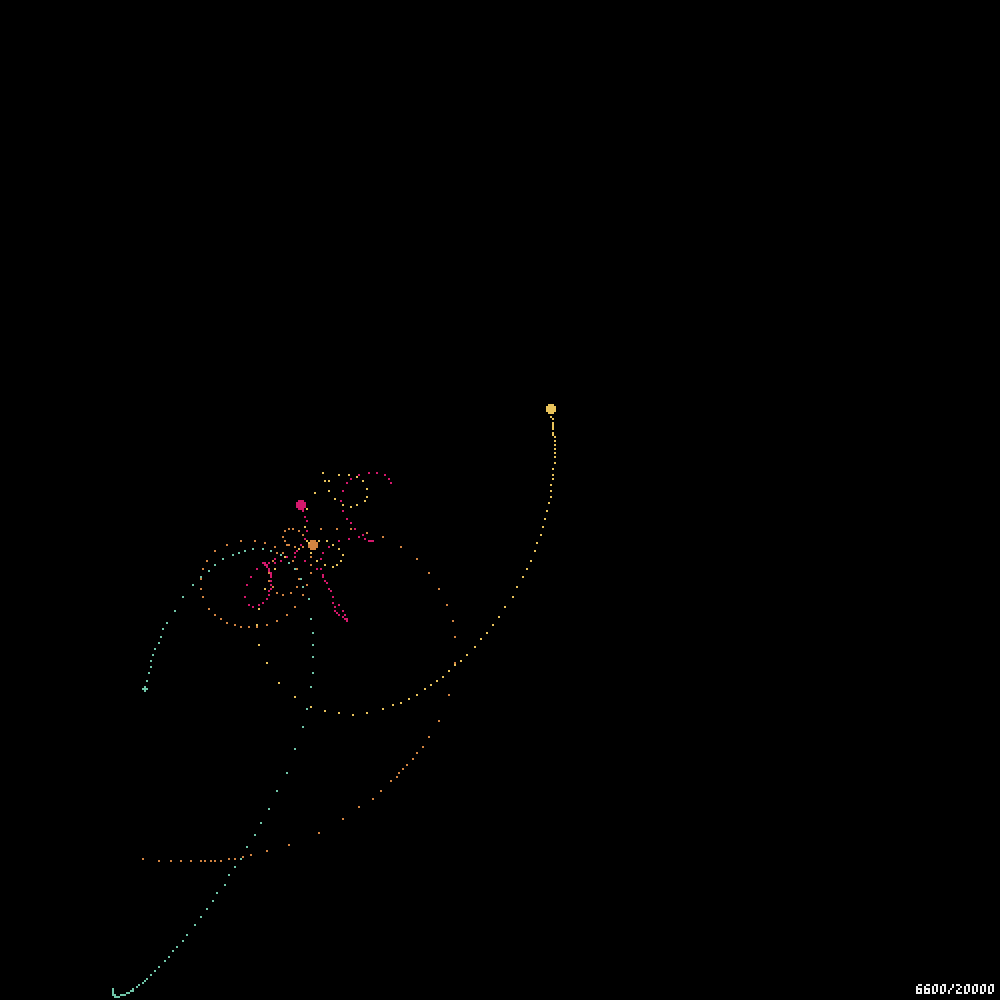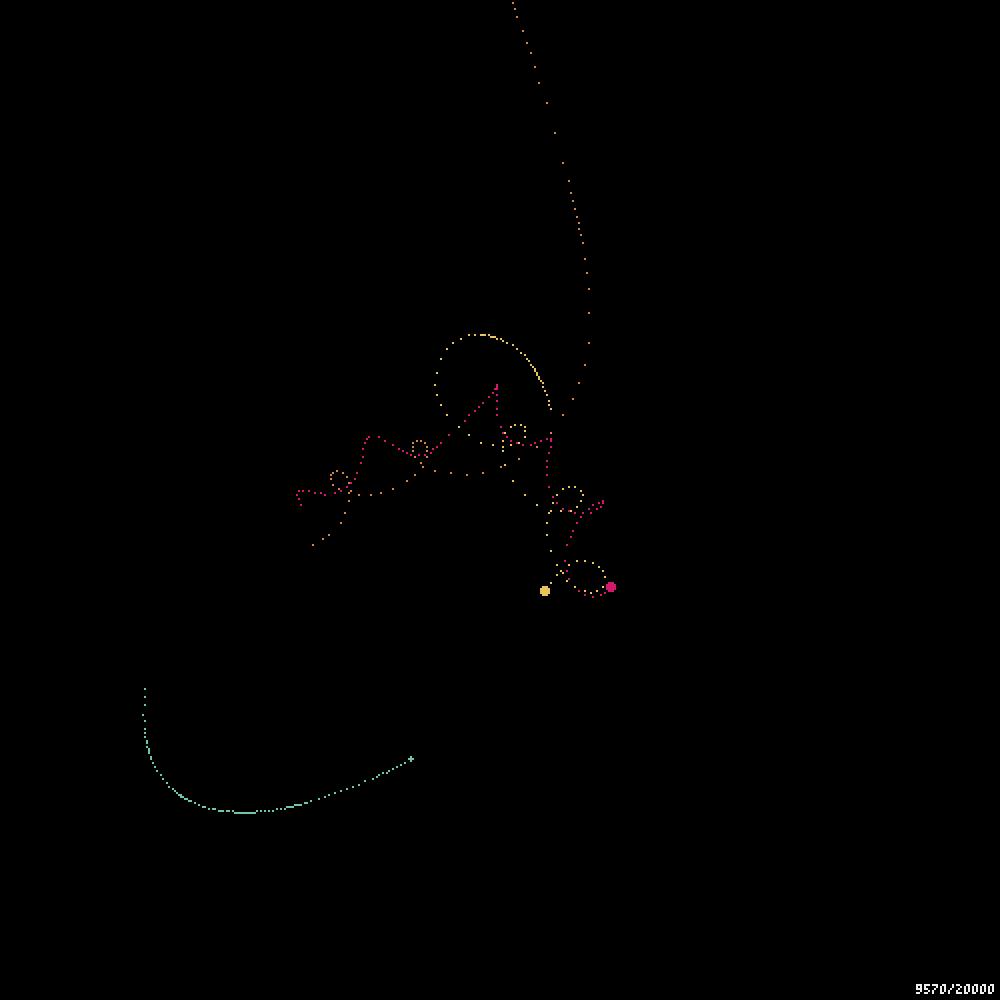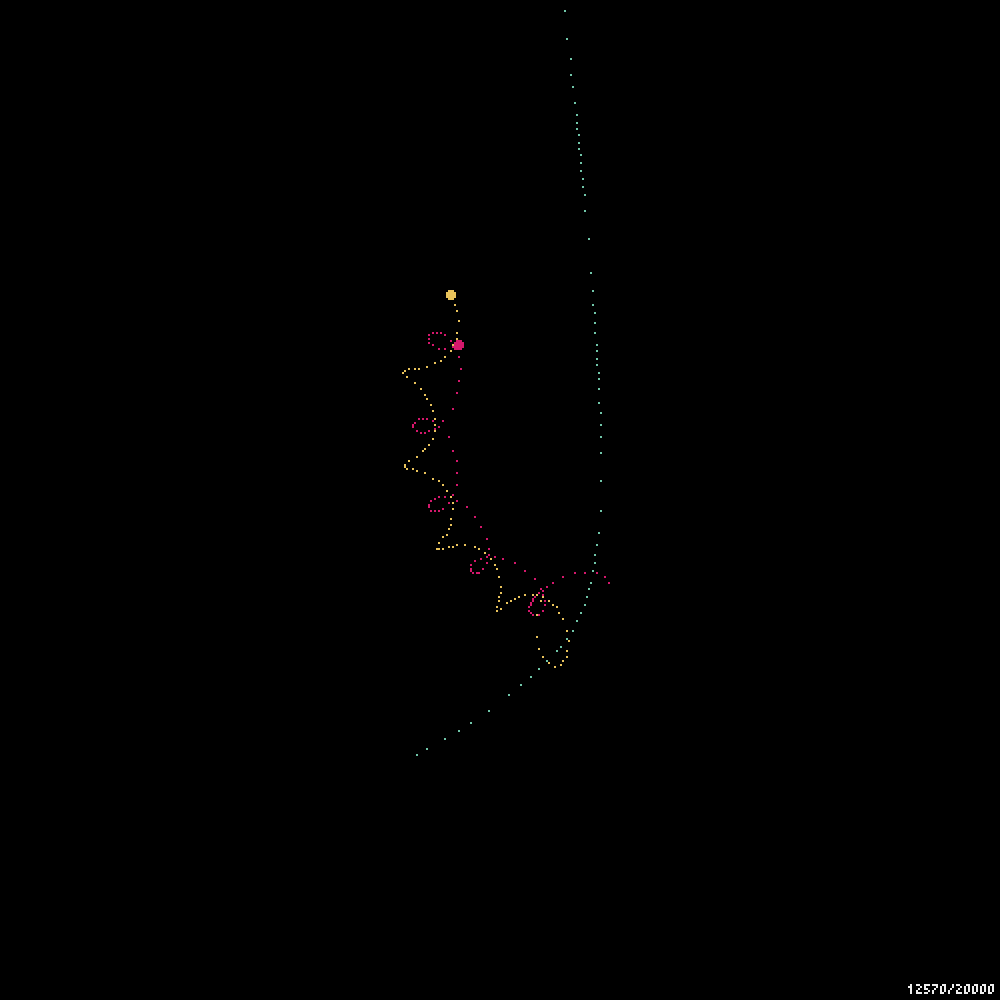
RKF45によるシミュレーション結果

やっぱり吹き飛ぶ三体星人。。。RIP

天体を色分けしたり、軌道のトレース機能を追加していい感じに、カオスな挙動を可視化できた！

実装コードはGitHubで公開した。

おもしろかったです（小並）